Оценка тесноты связи между количественными признаками, ранговые коэффициенты К. Спирмена и М. Кендела.

Оценк

а интенсивности связи между количественными признаками (и качественными) проводится с помощью непараметрических методов. В основу этих методов положен принцип нумерации значений статистического ряда. Каждый единицы совокупности присваивается порядковый номер в ряду, который будет упорядочен по уровню признака. С помощью этого ряд значений признака ранжируется, а номер каждой отдельной единицы будет её рангом.

Ранговые коэффициенты К. Спирмэна и М. Кендэла.

Ранговые коэффициенты Спирмэна и Кендэла применяют для изменения связи между ранжированными признаками. Эти методы применяют не только для качественных, но и для количественных показателей, особенно при малом объёме совокупности, так как непараметрические методы ранговой корреляции не связаны ни с какими ограничениями относительно характера распределения признака.

Метод Спирмена:

располагают варианты факторного признака по возрастанию – ранжируют единицы по значению признака Х;

для каждой единицы совокупности указывают ранг с точки зрения результативного признака У.

Если связь между признаками прямая, то с увеличением ранга признака Х ранг признака У также будет возрастать; при тесной связи ранги признаков Х и У в основном совпадут. При обратной связи возрастанию рангов признака Х будет, как правило, соответствовать убывание рангов признака У. В случае отсутствия связи последовательность рангов признака У не будет обнаруживать никакого порядка возрастания или убывания.

Теснота связи между признаками оценивается ранговым коэффициентом корреляции Спирмена:

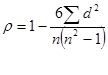
Где d – разность рангов признаков Х и У;

N – число наблюдаемых единиц.

В случае отсутствия связи р=0. При прямой связи коэффициент р – положительная правильная дробь, при обратной – отрицательная.

Кендэллом предложен другой показатель изменения корреляционной связи, также с использованием рангов признаков:

Упрощение расчётов Кендэла:

1. Ряд наблюдений располагается в возрастающем порядке по признаку Х с указанием соответствующих им рангов по признаку У.

2. Упорядоченная таким образом последовательность наблюдений берется как исходная для построения квадратной матрицы размерностью (n * n). Для заполнения матрицы по каждой паре наблюдений (i, j) сравнивают ранги признака У:

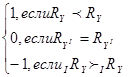
Cума элементов матрицы, расположенных выше главной диагонали, и есть искомое значение S.

При достаточном навыке расчет величины S можно выполнить, непосредственно сравнивая ранг Ry данного наблюдения с рангом Ry последующих наблюдений. Для каждого наблюдения подсчитываются Р – число случаев, когда ранг признака У у следующих наблюдений меньше, чем у данного, и Q – число случаев, когда у следующих наблюдений ранг признака У больше, чем у данного. Искомое наблюдение

Правильность условия контролируется соблюдением условия

Далее производится расчет по приведённой ранее формуле.

При достаточно больших n между значениями ранговых коэффициентов фиксируется соотношение:

Теоретико-методологические основы тестирования учебной деятельности при изучении преобладающих способностей человека. История развития тестирования
В последнее время социологи все чаще прибегают к использованию тестов в социологических исследованиях. В некоторых исследовательских ситуациях социолог прибегает к использованию тестов, когда ничем другим кроме тестов не может быть получе ...

Понятие и виды социальных пенсий
Социальное обеспечение занимает одно из ключевых определяющих мест в жизни государства и общества. Оно непосредственно зависит от развития экономики и теснейшим образом связано с политикой социального благополучия населения. Право россий ...

Новые формы семейных ценностей
Вовлечение в XIX веке женщины в профессиональную деятельность способствовало ее общественно-политической активности и отразилось на социально-экономическом статусе мужчин – все это, вместе взятое, положило начало кризису патерналистских ц ...